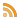Der Buchsatzspiegel
Der Aufbau einer Buchseite ist eine Wissenschaft für sich. Erstaunlich, geht es doch eigentlich nur um einen bedruckten Innenbereich und vier Ränder drumherum. Nun ja, ganz so einfach ist es nicht, wie wir sehen werden. Die Überlegungen zum Buchsatzspiegel sind durchaus kompliziert und stammen teilweise aus den grauen Vorzeiten des Buchsatzes. Wichtig sind sie besonders – aber nicht nur – für das äußere Erscheinungsbild eines Buches.
Mindestens genauso wichtig für das Erscheinungsbild – insbesondere für die Lesbarkeit des Buchtextes – sind die Schriftart, die Schriftgröße, die Zeilenlänge und der Abstand der Zeilen untereinander. Die Schrift und ihre Attribute haben direkte Auswirkungen auf den Satzspiegel: Die für eine bestimmte Schrift optimale Zeilenlänge sollte möglichst genau der Satzspiegelbreite entsprechen, Schriftgröße und Zeilenabstand entscheiden gemeinsam mit der Satzspiegelhöhe über die Zeilenanzahl pro Seite – und damit über die gesamte Seitenzahl und letztlich den Buchpreis. Alles hängt miteinander zusammen und muss für jedes einzelne Buchprojekt gut austariert werden.
An dieser Stelle soll es nun aber zunächst um den Aufbau einer Buch-Doppelseite gehen, also insbesondere um die Proportionierung des Satzspiegels und der Ränder.
Inhalt
↪ Grundsätzliches
↪ Goldener Schnitt
↪ Fibonacci-Zahlen
↪ Villardscher Teilungskanon
↪ Neunerteilung
↪ Fazit
↪ Beispiel
Grundsätzliches
Die zentrale Fläche einer Buchseite ist bedruckt. Sie wird „Satzspiegel“ genannt. „Buchsatzspiegel“ bezeichnet dagegen den gesamten Aufbau einer Buch-Doppelseite mit ihrer rechten Seite (Verso) und ihrer linken Seite (Recto). Außerhalb des Satzspiegels bleibt das Papier weiß. Dies ist der „Weißraum“, bestehend aus den vier Rändern, den Stegen: Bundsteg, Kopfsteg, Außensteg und Fußsteg.
Über die genauen Proportionen des Satzspiegels und der Stege gibt es ganze Abhandlungen, die meist mit mathematisch/geometrischen Ansätzen arbeiten. Sie alle haben das Ziel, ein für das menschliche Auge ästhetisch wirkendes Gesamtbild zu erzeugen. Moderne Wahrnehmungspsychologie spielt dabei genauso eine Rolle wie althergebrachte Theorien der Ästhetik – der Goldene Schnitt beispielsweise, der seit der Antike als ideales Prinzip ästhetischer Proportionierung gilt.
Allen hier vorgestellten Ansätzen ist gemeinsam, dass der Satzspiegel dasselbe Seitenverhältnis aufweist wie die Buchseite. Außerdem wird er nicht mittig darauf platziert. Die Stegbreiten steigen in der oben genannten Reihenfolge, zumindest sinken sie nicht (Bund <= Kopf <= Außen <= Fuß). Dafür gibt es eine Reihe handfester Gründe:
- Bundsteg < Außensteg: Bei einem aufgeklappten Buch wirken die beiden inneren Stege (Bundstege) optisch gemeinsam. Die beiden Satzspiegel (linke und rechte Buchseite) werden also durch die doppelte Bundstegbreite voneinander getrennt. Demgegenüber steht aber jeweils ein einzelner Außensteg. Wird jedem Außensteg etwa die doppelte Breite eines einzelnen Bundstegs gegeben (Faktor 2), ist das optische Gleichgewicht wieder hergestellt: Links und rechts jedes Satzspiegels wirkt die gleiche Randbreite. Durch die Wölbung der Buchseiten in der Mitte wirkt der innere Bereich allerdings etwas weniger breit, als er tatsächlich ist. Daher sollte der Außensteg auf keinen Fall noch größer dimensioniert werden als Faktor 2 (beim Goldenen Schnitt ist es etwa der Faktor 1,62).
- Kopfsteg < Fußsteg: Ein vertikal mittig angeordnetes Designelement wirkt optisch eher zu tief. Mittig wird es wahrgenommen, wenn es ein kleines Stück oberhalb der geometrischen Mitte platziert wird. Eine Methode, dieses „Stückchen“ exakt zu berechnen, kenne ich nicht; es ist jedenfalls ein sehr kleines Stückchen. Dieser Problematik kann man entgehen, indem man die geometrisch mittige Anordnung ganz verwirft und eine „Balancelinie“ findet, auf der angeordnet Elemente als „harmonisch zentral“ empfunden werden. Nach Wikipedia kann diese „optische Mitte“ bei einem Din-Blatt bei einer Höhe von 2x(Seitenhöhe-Seitenbreite) liegen, entsprechend 2xSeitenbreite - Seitenhöhe von oben. Auch ein Satzspiegel wirkt – bewusst aus der geometrischen Mitte angehoben – deutlich harmonischer.
- Außen- und Fußsteg sind die größten: An diesen beiden Stegen wird das aufgeklappte Buch beim Lesen normalerweise gehalten. Beide gemeinsam können somit als „Griffe“ des Buches angesehen werden. Je schmaler sie ausfallen, desto mehr stören die Daumen beim Lesen, da sie hier oder da in den Satzspiegel hineingreifen müssen.
Gerade im Bereich des Selfpublishings (aber nicht nur dort) finden sich viele Werke, bei denen der Satzspiegel nicht bewusst gewählt zu sein scheint – jedenfalls nicht nach buchgestalterischen oder auch nur ästhetischen Überlegungen. Vielmehr scheint der Preis je gedruckter Buchseite, die der Print-on-Demand-Dienstleister oder die Druckerei verlangt, das Hauptkriterium zu sein, denn oft ist der Satzspiegel schlicht zu groß gewählt, die Seitenränder bzw. Stege zu schmal (wodurch natürlich die Gesamtseitenanzahl und damit der Preis reduziert wird). Dies erzeugt leider den Eindruck von Enge oder Gedrängtsein. Der Anblick einer solchen Seite erschlägt mehr, als dass er erfreut. Klassische Buchsatzspiegel sehen dagegen vergleichsweise großen Weißraum vor. Bei ihnen nimmt er etwa dieselbe Fläche in Anspruch wie der Satzspiegel. Die Stege, insbesondere Außen und Fußsteg, fallen also sehr üppig aus. Das Ergebnis ist ein luftiges Erscheinungsbild, insbesondere im Zusammenspiel mit einem ausreichend großen Zeilenabstand. Der pure Anblick – und damit auch das Lesen – macht so auf einer unbewussten Wahrnehmungsebene Spaß.


Im Folgenden möchte ich einige Möglichkeiten vorstellen, einen Satzspiegel zu berechnen. Dabei geht es sowohl um klassische als auch moderne Wege, ein schönes Seitenlayout zu gestalten.
Goldener Schnitt
Ach ja, der Goldene Schnitt. Mindestens seit Euklid von Alexandria (3. Jhd. v. Chr.) geistert er durch die Menschheitsgeschichte und hält Designer aller Genres in seinem Bann. Architektur, Bildhauerei, Malerei, Fotografie und Buchsatz – überall findet der Goldene Schnitt Verwendung bei der Gestaltung von Proportionen. Seit Jahrhunderten interessieren sich auch Theologen und Philosophen für dieses „göttliche Prinzip“.

Dabei geht es beim Goldenen Schnitt schlicht darum, eine gegebene Gesamtlänge in zwei Teillängen aufzuteilen, und zwar derart, dass die entstehenden Proportionen als möglichst harmonisch empfunden werden – was auch immer das bedeutet. Konkret besagt der Goldene Schnitt, dass dieses Ziel erreicht ist, wenn sich die beiden Teillängen a und b so zu einander verhalten, wie die Gesamtlänge a+b zu a, dem größeren der beiden Teile. Mathematisch ausgedrückt:
a/b = (a+b)/a = Φ
Nach Umstellung der Gleichung, Lösung einer quadratischen Gleichung und einiger weiterer Erkenntnisse (z.B. 1/Φ = Φ-1) ergeben sich die folgenden Beziehungen:
a/b=Φ≈1,618a=(Φ-1) · (a+b)≈0,618 · (a+b)b=(2-Φ) · (a+b)≈0,382 · (a+b)
Zusammenfassend kann man sagen: Eine Gesamtlänge gilt dann als besonders harmonisch aufgeteilt, wenn ihre Teillängen etwa 62% und 38% entsprechen.
Doch genug der Mathematik. Wie kann der Goldene Schnitt nun auf eine Buchseite angewendet werden? Indem das goldene Verhältnis Φ ≈ 1,618 auf möglichst viele Längen des Buchsatzsspiegels übertragen wird. Denkbar ist hier:
- Satzspiegelbreite / (Bundsteg + Außensteg) = Φ
- Satzspiegelhöhe / (Kopfsteg + Fußsteg) = Φ
- Außensteg / Bundsteg = Φ
- Fußsteg / Kopfsteg = Φ
Ist die Papiergröße gegeben (das Buchformat), dann ergibt sich:
- Satzspiegelbreite = 0,62 · Papierbreite
- Satzspiegelhöhe = 0,62 · Papierhöhe
- Bundsteg = 0,38 · (0,38 · Papierbreite)
- Kopfsteg = 0,38 · (0,38 · Papierhöhe)
- Außensteg = 0,62 · (0,38 · Papierbreite)
- Fußsteg = 0,62 · (0,38 · Papierhöhe)
Optisch besonders wirksam ist hierbei, dass die gegenüberliegenden Stege jeweils im goldenen Verhältnis zueinander stehen. Dies funktioniert mit jedem Papierseitenverhältnis. Das Seitenverhältnis des Satzspiegels ist dabei immer genau dasselbe wie das des Papiers.


Der Weißraum ist bei diesem Verfahren sehr groß, zu groß für heutige Maßstäbe (üblich waren solche Stege eher im Mittelalter). Man kann allerdings auf die beiden ersten Gleichungen verzichten und Satzspiegelbreite und -höhe größer wählen. Werden die Stege weiterhin ins goldene Verhältnis gesetzt, wird der Buchsatzspiegel auch weiterhin sehr harmonisch wirken.
Fibonacci-Zahlen
Mithilfe der berühmten Fibonacci-Folge kann die Aufteilung nach dem Goldenen Schnitt sehr einfach bestimmt werden. Die ersten Zahlen dieser Folge lauten: 1, 1, 2, 3, 5, 8, 13, 21, 34, ... Jede Zahl ergibt sich aus der Summe der beiden vorhergehenden (1+1=2; 1+2=3; 2+3=5; 3+5=8; ...). Spannend ist dabei, dass sich das Verhältnis einer Zahl zu ihrer Vorgängerin dem goldenen Verhältnis von Φ ≈ 1,618 annähert, um so genauer, je größer diese Zahlen sind (2/1=2; 3/2=1,5; 5/3≈1,67; 8/5=1,60; 13/8≈1,63; 21/13≈1,61; 34/21≈1,62; ...). Jedes dieser Zahlenpaare ergibt also mehr oder weniger genau das Verhältnis, das der Goldene Schnitt beschreibt.
Wie kann man diese Zahlen einsetzen? Anstatt wie oben das Verhältnis Φ = 1,618... zu verwenden, kann man stattdessen in genügend guter Näherung benachbarte Fibonacci-Zahlen wählen. Praktisch teilt man das Buchblatt in ein passendes Raster aus Rechtecken auf und kann anschließend die Stegbreiten einfach abzählen. Beispielhaft ist das folgende Vorgehen:
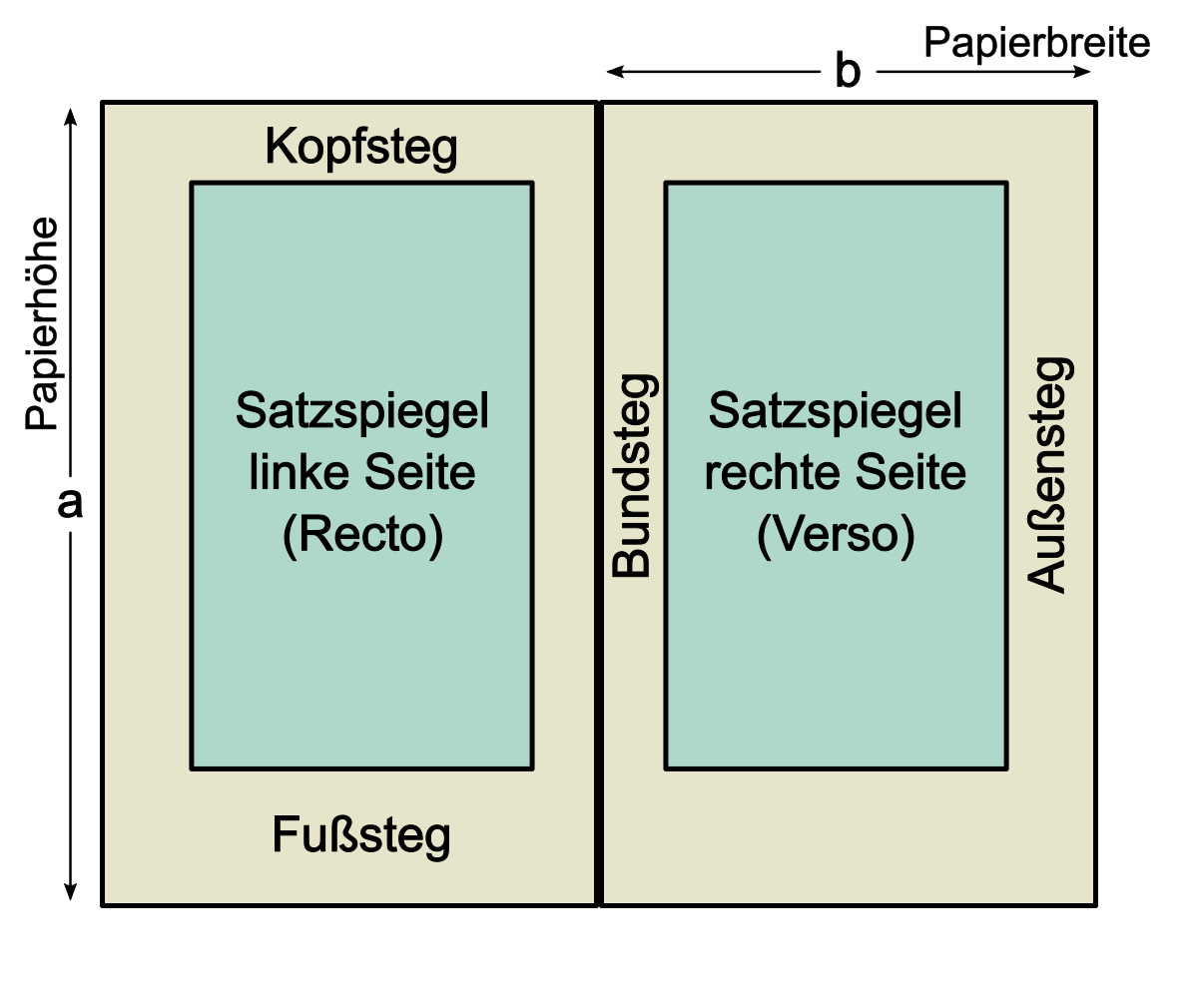
Man unterteilt die Seite vertikal in 34 Einheiten und horizontal in 21. Für die Satzspiegelhöhe werden anschließend 21 vertikale Einheiten gewählt und für die Satzspiegelbreite 13 horizontale Einheiten. Damit ist das Verhältnis zwischen Satzspiegelmaßen und Weißraum 21:13 bzw. 13:8. Der Innensteg erhält drei Einheiten, Außen- und Kopfsteg je fünf und der Fußsteg acht. Damit haben die Stege ein Verhältnis von 8:5 bzw. 5:3. Jedes dieser Verhältnisse entspricht dabei annähernd dem Goldenen Schnitt. Bildet das Raster Quadrate, dann ist auch das Seitenverhältnis des Papiers und das des Satzspiegels golden (34:21 bzw. 21:13).
Das gleiche Vorgehen ist auch mit feinerem oder gröberem Raster möglich. Die Genauigkeit der Annäherung an den Goldenen Schnitt nimmt dabei zu oder ab.



Villardscher Teilungskanon
Auf den Dombaumeister Villard de Honnecourt (geboren um 1200) geht eine geometrische Satzspiegel-Konstruktion zurück, die in vielen klassischen Schriften verwendet wurde, z.B. auch bei der 42-zeiligen lateinischen Gutenberg-Bibel („B42“) aus dem 15. Jahrhundert. Anders als häufig behauptet hat diese Methode mathematisch rein gar nichts mit dem Goldenen Schnitt zu tun. Das bestimmende Verhältnis ist 2:1 und entspricht damit (rein zufällig) dem kleinstmöglichen Fibonacci-Zahlenpaar, das sich dem Goldenen Schnitt mit der geringsten Genauigkeit annähert. Dennoch liefern beide Methoden Buchsatzspiegel, die zumindest für das ungeübte Auge ähnlich sind.
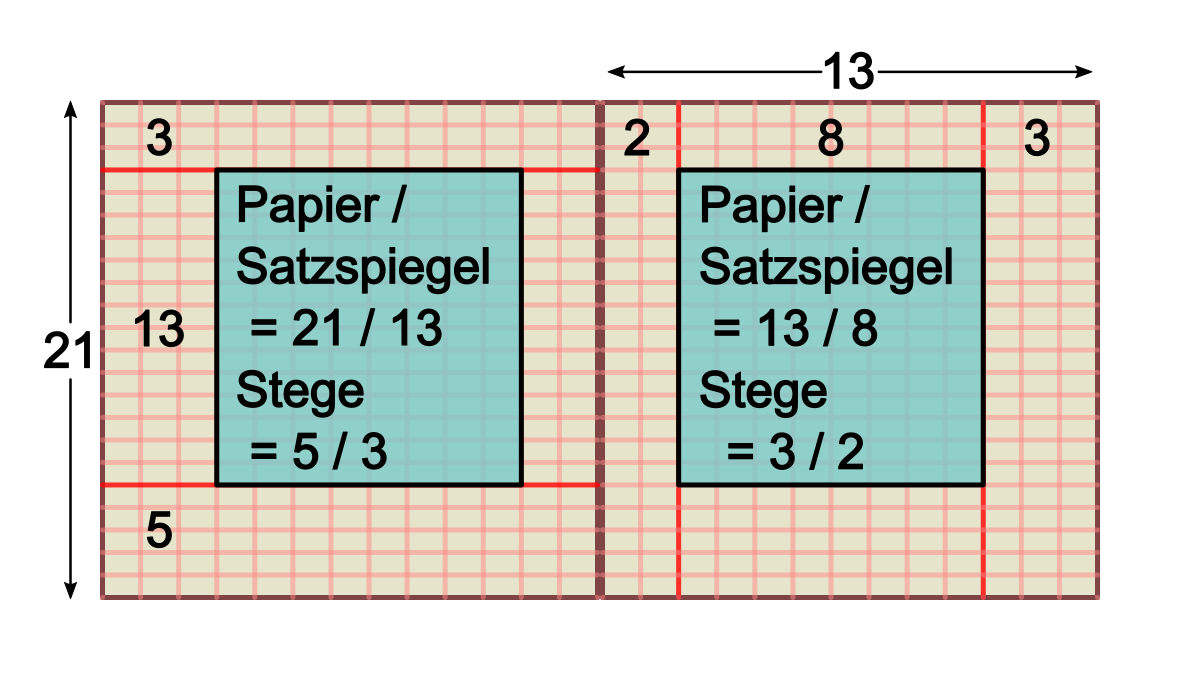
Die Konstruktion basiert zunächst auf Diagonalen: Beide Diagonalen der Buch-Doppelseite sowie eine Diagonale durch jede Einzelseite (von oben in der Buchmitte zur jeweiligen unteren Außen-Ecke). Der rechte Satzspiegel ergibt sich aus zwei weiteren Linien: vom Diagonalen-Schnittpunkt auf der rechten Seite senkrecht bis zur Oberkante des Blatts, von dort hinüber zum Diagonalen-Schnittpunkt auf der linken Seite. Der Schnittpunkt dieser letzten Linie mit der Seiten-Diagonale der rechten Seite ergibt den Startpunkt A. Dieser Punkt wird als oberste linke Ecke des Satzspiegels definiert. Von dort verläuft die Satzspiegel-Oberkante waagerecht nach außen bis zur Doppelseiten-Diagonale. Hier ergibt sich der Punkt B, der die obere rechte Ecke darstellt. Von hier aus senkrecht nach unten bis zur Seiten-Diagonale ergibt Punkt C, die untere rechte Satzspiegel-Ecke. Die untere linke Ecke ergibt sich automatisch aus Punkt A und C.
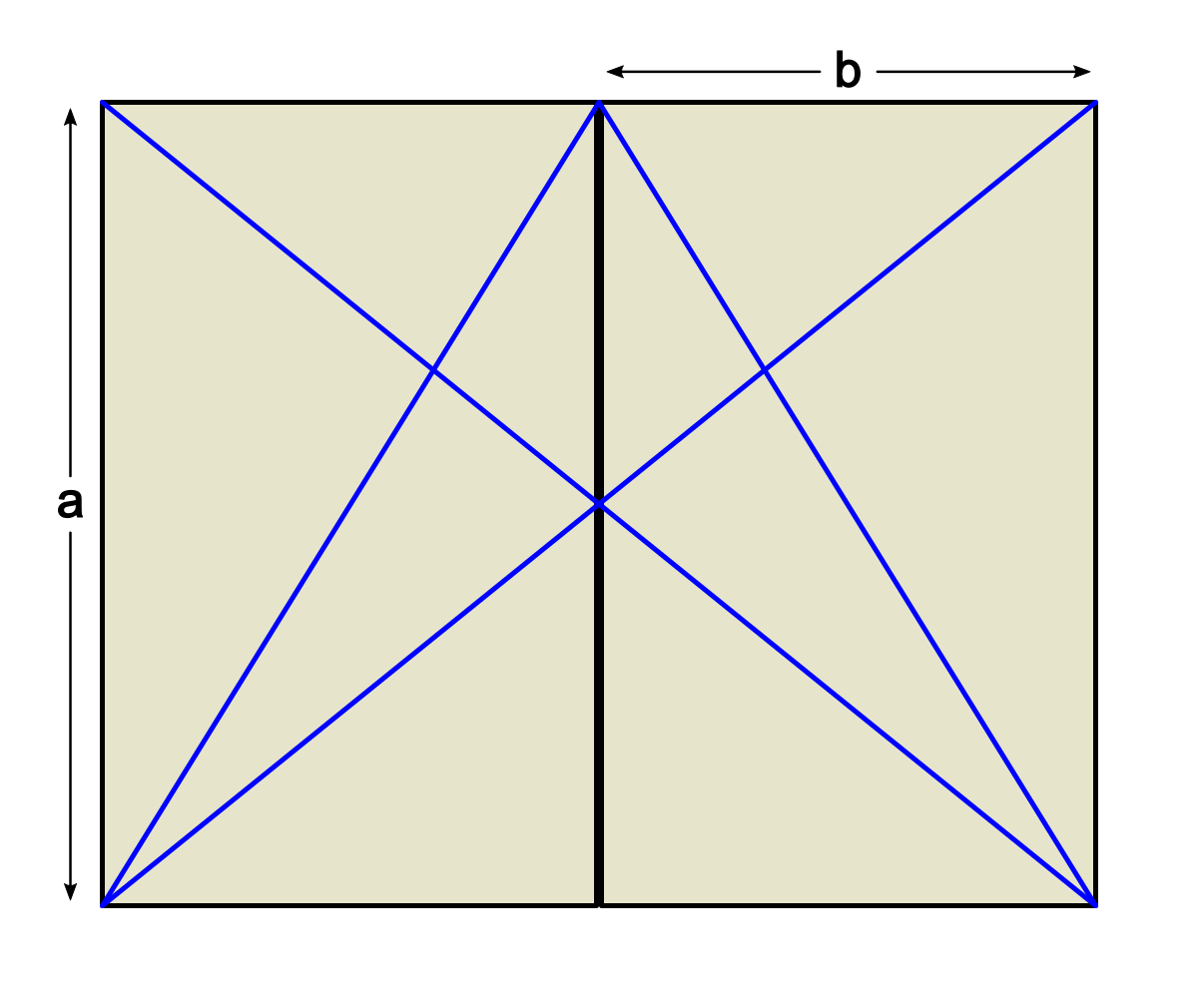


Mit ein wenig analytischer Geometrie ergeben sich folgende Verhältnisse:
- Satzspiegelbreite / (Außensteg + Bundsteg) = 2/1
- Satzspiegelhöhe / (Fußsteg + Kopfsteg) = 2/1
- Außensteg / Bundsteg = 2/1
- Fußsteg / Kopfsteg = 2/1
Das Ganze funktioniert übrigens mit beliebigen Seitenverhältnissen des Buchformats. Dieses Verhältnis bleibt auch für den Satzspiegel erhalten. Auch quadratische Seiten sehen gut aus nach Villard; und historische Bibeln ebenso.



Wie am Beispiel der Gutenbergbibel ersichtlich ist, bietet auch der Villardsche Teilungskanon viel Weißraum (bei Gutenberg ist der Weißraum allerdings schön bunt). Wer einen größeren Satzspiegel benötigt, kann auch bei diesem Verfahren das Verhältnis Satzspiegelmaße / Weißraummaße variieren, ohne dass die Steg-Verhältnisse sich verändern. Dafür verzichtet man auf die letzten beiden Linien der Diagonalen-Konstruktion und wählt den Startpunkt A frei auf der Seiten-Diagonale; die Punkte B und C werden wie gehabt ermittelt.
Sehr schnell gerät auf diese Weise der Bundsteg allerdings zu klein. Überhaupt platziert das gesamte Verfahren den Satzspiegel für meinen Geschmack zu weit nach innen, aber auch zu weit nach oben. Dennoch ist es immer wieder anzutreffen, insbesondere in Form der Neunerteilung.
Neunerteilung
Betrachtet man die Konstruktions-Ergebnisse nach Villard genauer, insbesondere das überall auftretende Verhältnis 2/1, dann kommt man schnell darauf, dass all dies nichts anderes ist als eine simple Rasterkonstruktion mit 9 Kästchen horizontal wie vertikal. Der Punkt A befindet sich immer bei 1/9 der Buchseite. Der Bundsteg ist ein Kästchen breit, der Außensteg zwei. Die Satzspiegelbreite ist (1+2)·2/1=6 Kästchen. Vertikal ist alles entsprechend. Das Seitenverhältnis des Satzspiegels entspricht natürlich auch hier dem der Buchseite.


Die beliebte „Neunerteilung“ entspricht also dem strengen Aufbau nach Villard (inkl. der beiden zusätzlichen Konstruktionslinien) und stellt nur wenige mathematische Anforderungen. Wie oben schon betrachtet, bietet selbst die Gutenbergbibel die Neunerteilung.
Auch bei diesem simplen Verfahren gibt es die Möglichkeit, den recht üppigen Weißraum zu verkleinern: Man nimmt einfach nicht neun, sondern z.B. zwölf Kästchen und spricht entsprechend von der Zwölferteilung. Denkbar sind viele weitere Einteilungen mit andern Kästchenzahlen, solange die Stege ein bzw. zwei Kästchen in Anspruch nehmen (Achtung: Auch hierbei wird der Bundsteg schnell zu klein!). Das Stegverhältnis von 2/1 bleibt stets erhalten und ist neben dem Seitenverhältnis die einzige feste Eigenschaft dieser Methode.
Fazit
Es ist schon erstaunlich, dass man sich mit Mathematik und analytischer Geometrie auseinandersetzt, um letztlich bei einem kinderleichten 9x9- oder 12x12-Raster zu landen. Und das alles, um einen Satzspiegel zu bestimmen, der sich „harmonisch“ in die Buchseite einfügt. Die Typografie braucht feste Regeln, um einheitliche Ergebnisse zu liefern – aber auch akzeptierte Ergebnisse. Damit will ich sagen, dass auch der Satzspiegel Moden unterliegt. So sehr der Goldene Schnitt auch als göttliches Prinzip gehyped wurde, so sehr hat man ihn dennoch oft ignoriert oder selbstherrlich gerundet. Und es war okay. Nichts wird schließlich so heiß gegessen, wie es gekocht wird. Ob nun ein Steg-Verhältnis von 1,618/1 oder 2/1 – alles hat seine Freunde gefunden in den vergangenen Jahrhunderten. Selbst an 1/1 haben wir uns gewöhnt, seit Microsoft das Textsatzprogramm Word erfunden hat und die Seitenränder mit vier gleichen Werten vorbelegt hat. Wer kommt schon auf die Idee, diesen Standard anzupassen?
Nun gut, vier gleich große Ränder mögen bei einem Din-a-4-Briefbogen in Ordnung sein, ein schönes Buch werden sie nicht hervorbringen. An Villard und der Neunerteilung kritisierte ich bereits, dass der Satzspiegel zu weit aus der Mitte ragt; zumindest der Bundsteg ist mir tendenziell zu schmal. Der Goldene Schnitt aber, der aus der Antike stammt, scheint tatsächlich eine gute Richtschnur zu sein, auch heute noch – im rational-ökonomischen Zeitalter – schöne Bücher zu erzeugen. Die absolute Satzspiegelgröße könnte allerdings schon etwas größer sein.
Wie so oft heißt es also, einen persönlichen Kompromiss zu finden – und an der Stelle verlassen wir wieder den Bereich der typografischen Regeln. Tatsächlich scheint sich hier der Kreis dieses langen Artikels zu schließen. Der Goldene Schnitt scheint ein guter Ausgangspunkt zu sein, doch letztlich bleiben nur die ganz oben genannten Kriterien:
- Das Seitenverhältnis des Satzspiegels entspricht dem der Buchseite
- Bundsteg < Außensteg, damit die optisch doppelt wirkenden Bundstege ausgeglichen werden.
- Kopfsteg < Fußsteg, um dem Problem der optischen Mitte zu begegnen
- Außen- und Fußsteg sind die größten, damit sie als „Buchgriffe“ dienen können
Beispiel
Niemand zeichnet heute noch eine Diagonalenkonstruktion oder ein Raster auf eine Buchseite. Das Einstellen des Buchsatzspiegels geschieht heute in Computer-Dialogfenstern, in denen die Maße der vier Seitenränder verlangt werden. Diese gilt es zu berechnen. Dafür benötigen wir ein paar Multiplikationen.
Als Beispiel wähle ich hier meinen Kurzgeschichten-Band „Märzchen im November“. Ich habe ihn 2015 als mein erstes Buch im Selbstverlag entworfen. Auch meine beiden Folgebände habe ich mit denselben Maßen gestaltet. Damals bin ich etwa folgendermaßen vorgegangen:
Das Buch hat das Format 19x12cm. Um hierin den Buchsatzspiegel zu gestalten, beginne ich mit dem Goldenen Schnitt (b=Breite, h=Höhe, w=Weißraum, s=Steg):
bpapier=120mmbspiegel=0,62 · bpapier=74mmwhorz=bpapier - bspiegel=46mmsaußen=0,62 · whorz=29mmsbund=whorz - saußen=17mmhpapier=190mmhspiegel=0,62 · hpapier=118mmwvert=hpapier - hspiegel=72mmsfuß=0,62 · wvert=45mmskopf=wvert - sfuß=27mm
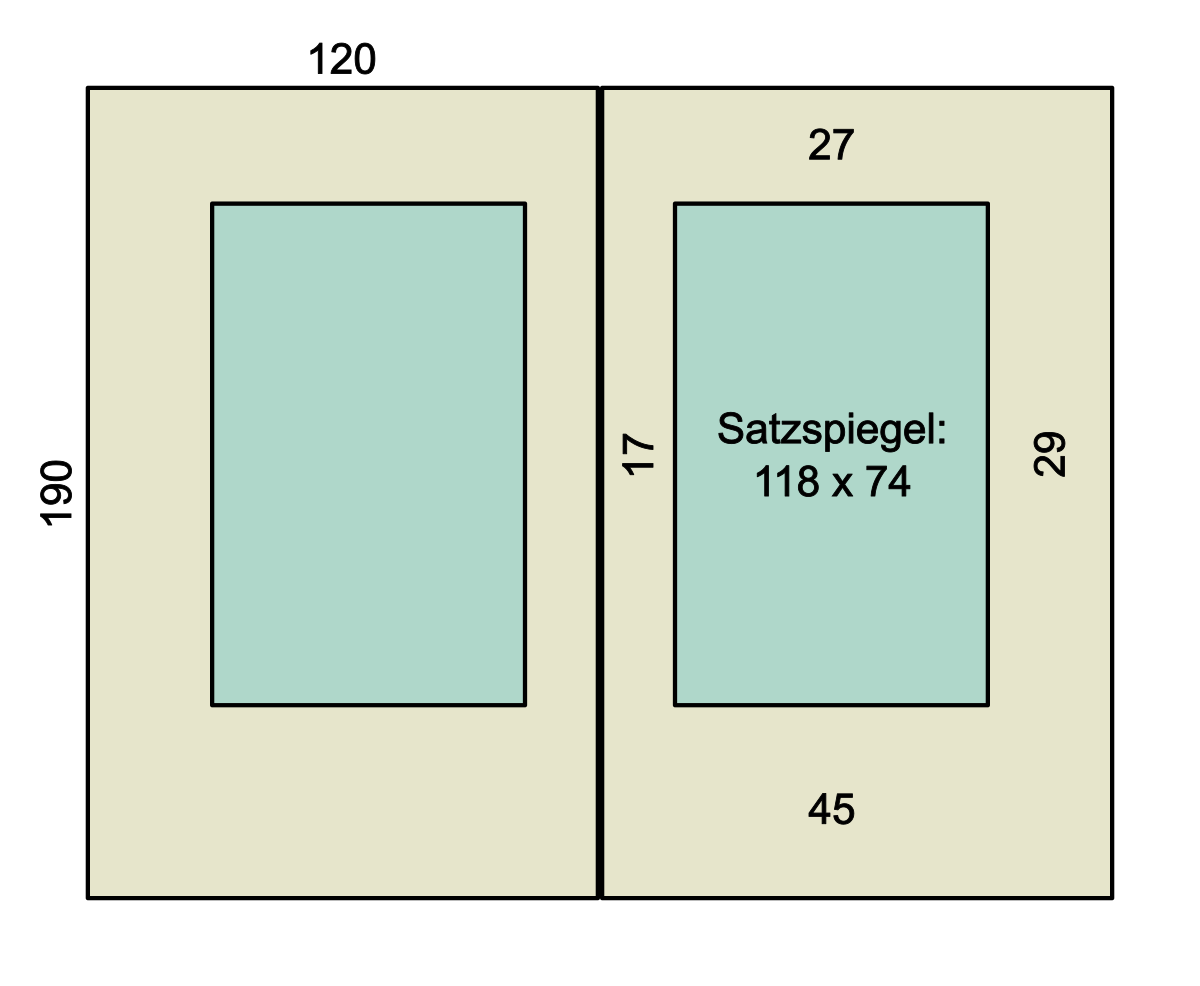
Mit diesen Werten wird es ein außergewöhnlich schönes Buch. Aber auch außergewöhnlich teuer, da mein Satzspiegel sehr klein ist und die Seitenzahl in die Höhe treibt. Außerdem ist die Zeilenlänge (Satzspiegelbreite) mit 74mm sehr klein für meine gewünschte Schriftgröße von 11,75pt. Ich entscheide mich für gut 1cm mehr Textbreite und wähle 86mm. Diesen Wert setze ich – dem Goldenen Schnitt zum Trotz – fest, da mir damit die Zeilenlänge zusagt. Damit beginne ich meine Rechnung von vorn (die Satzspiegelhöhe errechne ich mit Hilfe des Seitenverhältnisses der Buchseite):
bpapier=120mmbspiegel=86mmwhorz=bpapier - bspiegel=34mmsaußen=0,62 · whorz=21mmsbund=whorz - saußen=13mmhpapier=190mmhspiegel=bspiegel·(hpapier/bpapier)=136mmwvert=hpapier - hspiegel=54mmsfuss=0,62 · wvert=33mmskopf=wvert - sfuß=21mm
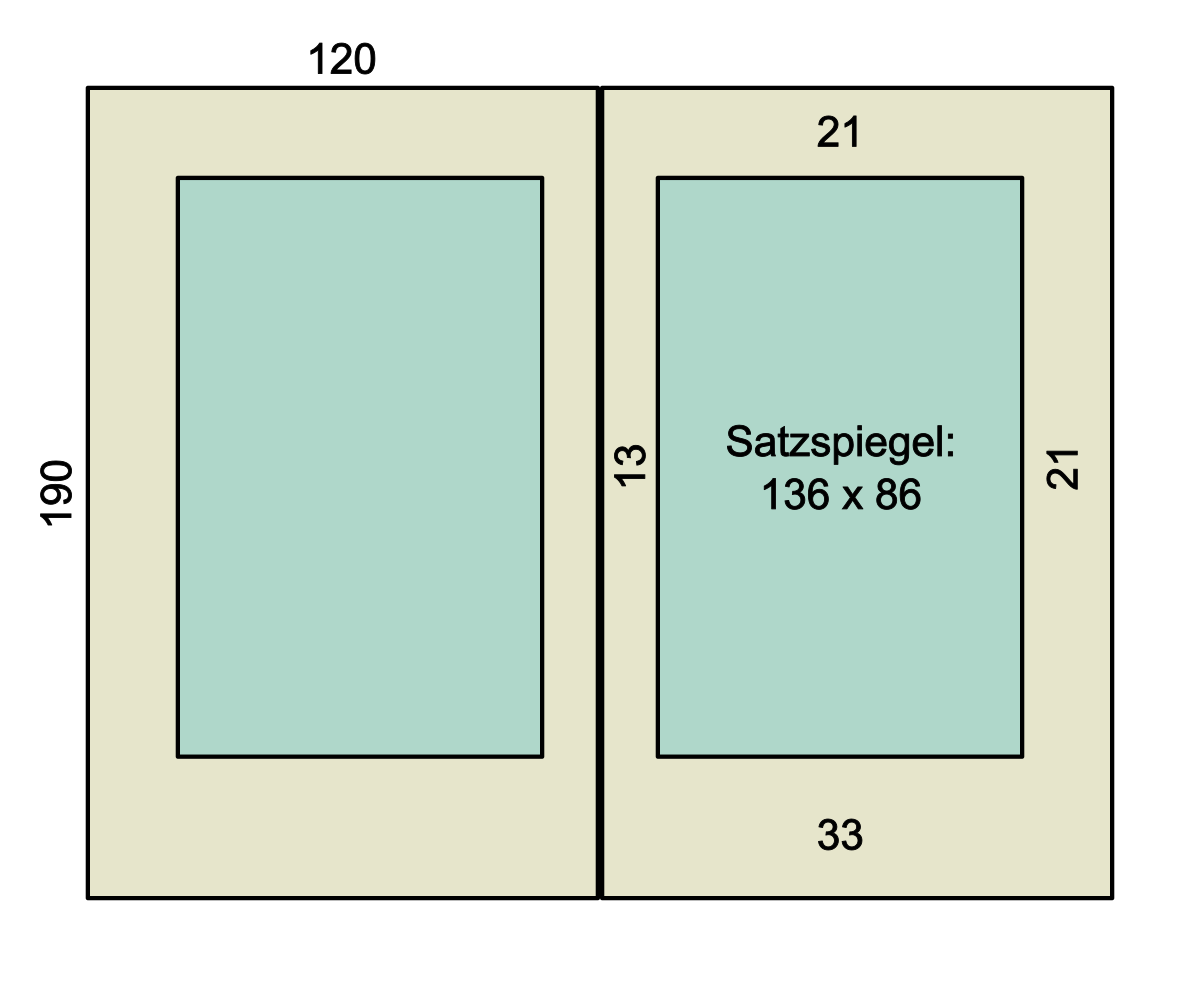
Das ist eigentlich schon ganz schön. Doch zwei Dinge passen mir noch nicht: Erstens liebe ich breite Bundstege, und zweitens ist mir der Fußsteg noch etwas übertrieben groß. Um den Bundsteg zu vergrößern, verschiebe ich den Satzspiegel um 3mm nach außen. Den Fußsteg reduziere ich einfach um 4mm auf 29mm. Als Ergebnis erhalte ich folgende Rechnung:
bpapier=120mmbspiegel=86mmsaußen = 21mm - 3mm=18mmsbund = 13mm + 3mm=16mmhpapier=190mmhspiegel = 136mm + 4mm=140mmsfuß = 33mm - 4mm=29mmskopf=21mm
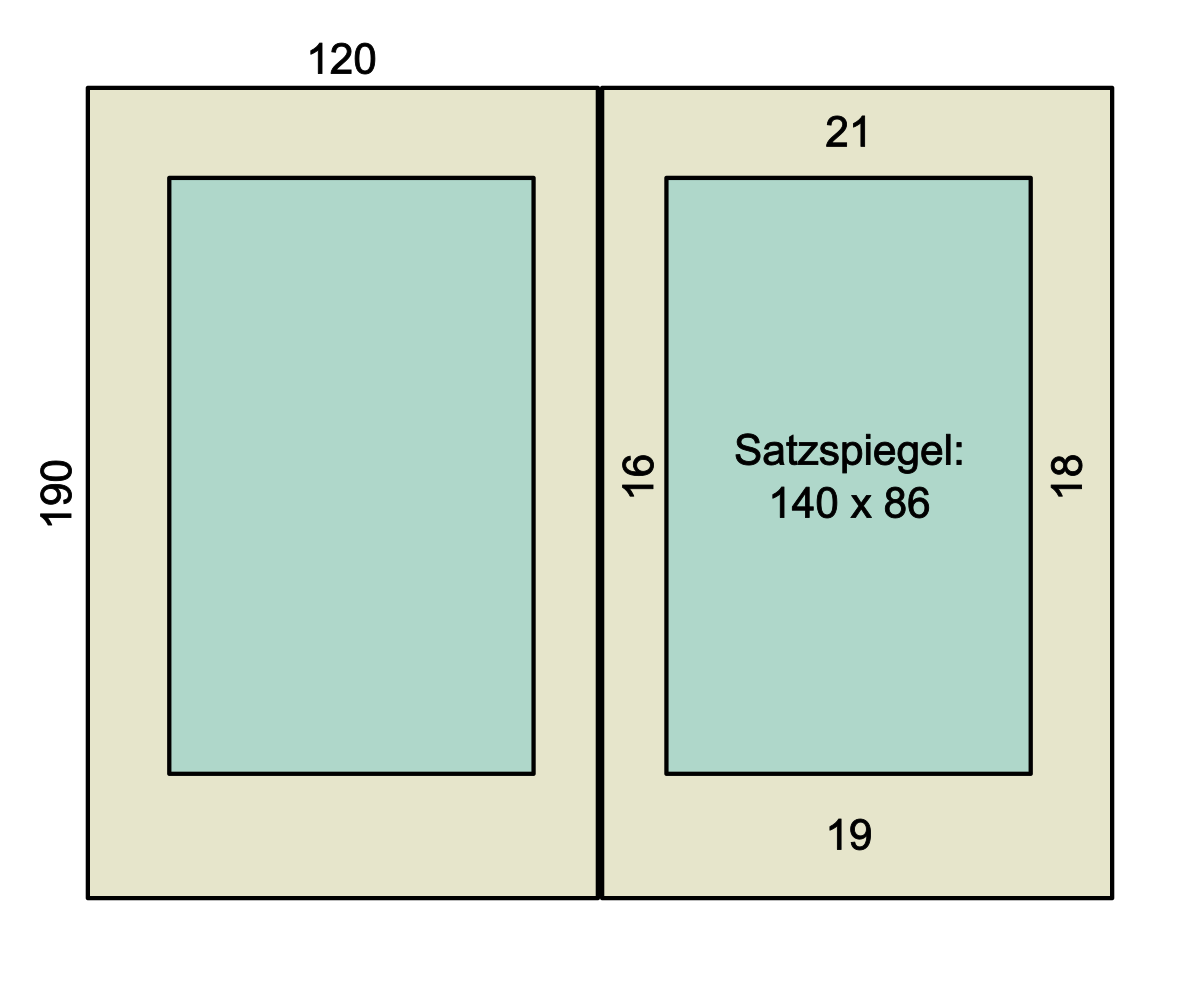
Das Verhältnis Außensteg/Bundsteg ist 18/16 = 1,125 und Fußsteg/Kopfsteg beträgt 29/21 = 1,38. Das ist beides zugegebenermaßen sehr klein. Theoretisch viel zu klein. Doch dadurch, dass das Buch bei meinem Hersteller sehr stramm gebunden wird, fällt die Wölbung in der Buchmitte sehr stark aus und verschlingt einen großen Teil der Bundstege. Aus dem gleichen Grund ist auch der Seitenfächer rechts und links sehr breit und wirkt optisch als Außensteg mit. Und der Kolumnentitel am oberen Buchrand füllt den Kopfsteg so sehr an, dass er ein bisschen mehr Fläche vertragen kann.

Man sieht, der Teufel steckt oft im Detail, und bis der optimale Buchsatzspiegel gefunden ist, braucht es oft mehrere Probedrucke. Ein Kompromiss zwischen Harmonie, Luftigkeit und den Buchkosten ist nicht leicht zu finden. Das ist völlig normal und sollte niemanden entmutigen.